Spectacular Tips About How Many Nodes Are In One Wave
Standing Wave Nodes And Antinodes
Understanding Waves
1. What Exactly is a Wave, Anyway?
Alright, let's talk waves. No, not the kind you catch at the beach, although the physics are surprisingly similar! We're talking about waves in the physics sense — those disturbances that transfer energy through a medium (like water, air, or even a string) or through space itself (like light!). Think of it as a ripple effect, but with some fascinating mathematical underpinnings.
Imagine dropping a pebble into a pond. You see those circular ripples moving outwards? Each ripple is a wave, carrying the energy of the pebble's impact. Now, these waves have highs (crests) and lows (troughs), and the distance between two crests (or two troughs) is what we call the wavelength. But where do nodes fit into all this?
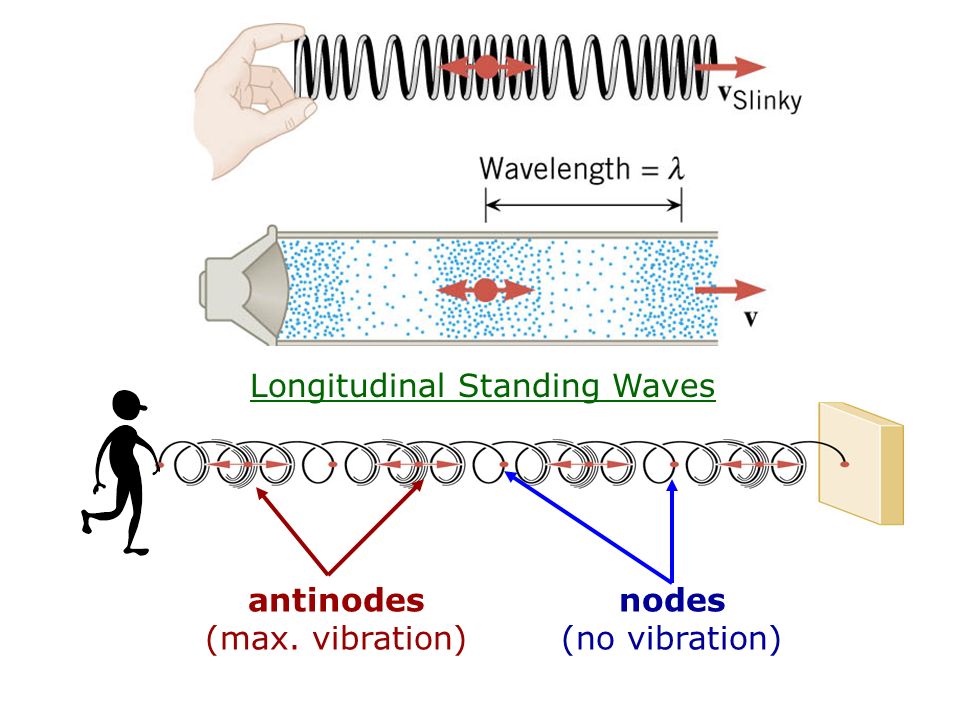
Before we dive into nodes, let's just clarify one thing: waves come in different forms. There are transverse waves, like those water ripples or light waves, where the disturbance is perpendicular to the direction the wave is travelling. Then there are longitudinal waves, like sound waves, where the disturbance is parallel to the direction of travel. Nodes behave similarly in both types, but visualizing them is often easier with transverse waves.
Think of it like this: a wave is like a cosmic dance, a beautiful and complex choreography of energy and movement. And nodes? Well, nodes are the still points in that dance, the places where the energy seems to disappear, momentarily frozen in time.
2. Nodes
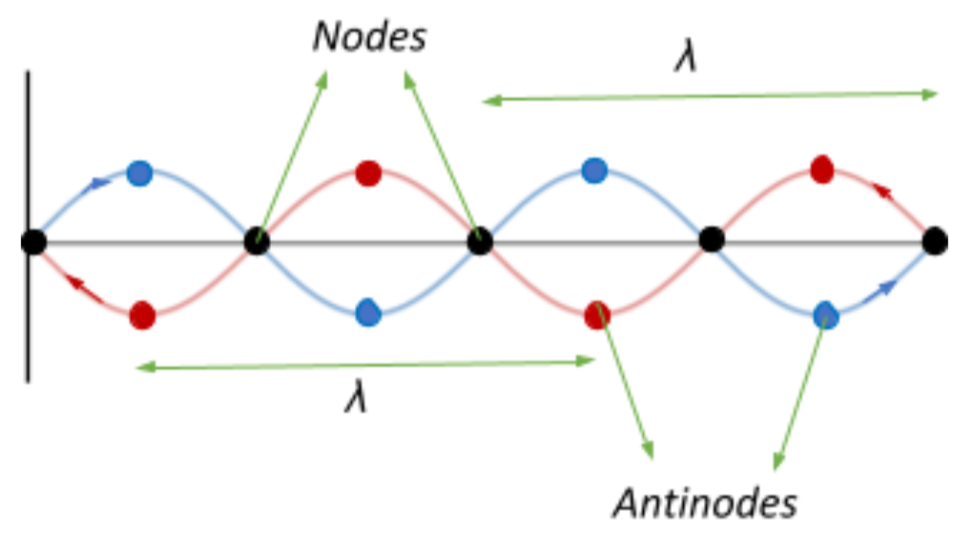
Okay, so what's a node? Simply put, a node is a point along a standing wave where the wave has minimum amplitude. In other words, it's a point that doesn't move (much) at all. Think of a guitar string vibrating. There are certain points along the string that barely move, even when the rest of the string is swinging wildly back and forth. Those points are nodes!
Let's use our water wave analogy again. If you could somehow freeze the water wave at a particular instant, you'd see crests and troughs. But there would also be points along the wave where the water level is at its normal, undisturbed level. These points, where the displacement from the equilibrium position is zero, are the nodes.
Nodes aren't just theoretical concepts; they're real and measurable. Scientists and engineers use them all the time when designing musical instruments, antennas, and all sorts of other devices that rely on wave behavior. Understanding where nodes are located is crucial for controlling and manipulating waves.
It's actually kind of cool to think about. In a world of constant motion and change, nodes represent pockets of stability. They're like the eye of the storm, the quiet center amidst the chaos. They are a testament to the fascinating and often counterintuitive nature of physics.
3. How Many Nodes are in One Wave? The Big Question!
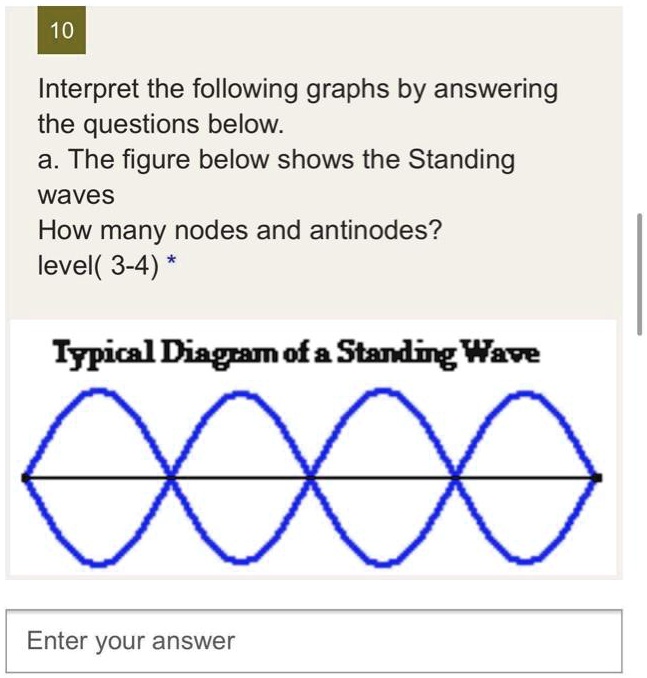
Alright, let's get down to brass tacks. How many nodes are in "one wave"? This is where it gets a little tricky, because the answer depends on what we mean by "one wave." Let's consider a standing wave fixed at both ends, like our guitar string example. The simplest standing wave, called the fundamental mode (or the first harmonic), has nodes at both ends and one node in the middle. This is half of a full wavelength.
So, for a half wavelength standing wave, there are three nodes. To get a full wavelength standing wave (the second harmonic), you'd have nodes at both ends and two nodes in between. That's four nodes in total! This is actually one full wavelength of a sine wave (two humps one up, one down), fixed at both ends.
If we're talking about a traveling wave — a wave that's moving freely through space — things get a little different. We don't typically talk about the number of nodes "in" the wave, because the wave is constantly moving. However, we can talk about the distance between nodes, which is half the wavelength. So, in one wavelength of a traveling wave, you could say there are two "potential" node locations, if you were to stop the wave and measure.
Confused yet? Don't worry, wave physics can be a bit mind-bending! The key takeaway is that the number of nodes depends on the context: whether it's a standing wave or a traveling wave, and how we define "one wave."
4. Standing Waves vs. Traveling Waves
To clear things up, let's quickly review the difference between standing and traveling waves. A traveling wave is a wave that propagates through a medium or space, transferring energy from one point to another. Think of a wave moving across the ocean or a pulse traveling down a rope. They move.
A standing wave, on the other hand, appears to stay in one place. It's formed when two waves of the same frequency traveling in opposite directions interfere with each other. This interference creates points of maximum amplitude (antinodes) and points of minimum amplitude (nodes). Guitar strings, organ pipes, and microwave ovens all rely on standing waves to function.
The number of nodes is inherently linked to the boundary conditions of the system. For instance, a string fixed at both ends must have nodes at those fixed points. This constraint dictates the possible wavelengths (and therefore the frequencies) of the standing waves that can exist on the string.
So, while both types of waves are essential for understanding the world around us, their node behavior is distinct. Remember: traveling waves travel, while standing waves stand (relatively) still, creating a pattern of nodes and antinodes. This pattern is key to understanding their properties and applications.
5. Practical Applications and Real-World Examples
Now that we understand the basics, let's explore some practical applications of nodes. As mentioned earlier, musical instruments are a prime example. Guitar strings, violin strings, and even the air columns in wind instruments all rely on the formation of standing waves to produce sound. Musicians manipulate the position of nodes by pressing down on strings or opening and closing holes, effectively changing the wavelength and therefore the pitch of the sound.
Another important application is in antenna design. Radio antennas, for example, are carefully designed to create standing waves with specific node and antinode patterns. These patterns determine the antenna's radiation characteristics, such as its directionality and gain. Engineers precisely control the placement of nodes to optimize the antenna's performance.
Nodes also play a crucial role in microwave ovens. Microwave ovens use standing waves of microwave radiation to heat food. The food is placed in the oven so that it is exposed to the antinodes of the standing wave, where the microwave energy is most intense. The nodes, on the other hand, are points of minimal energy, which is why food doesn't cook evenly if it's not rotated. Without understanding node placement, we would have very poorly cooked meals!
From musical instruments to communication technology to cooking appliances, nodes are everywhere! They are a fundamental aspect of wave behavior that has countless applications in our daily lives. So, the next time you strum a guitar or heat up a frozen pizza, remember the humble node — the silent partner in the dance of energy and movement.
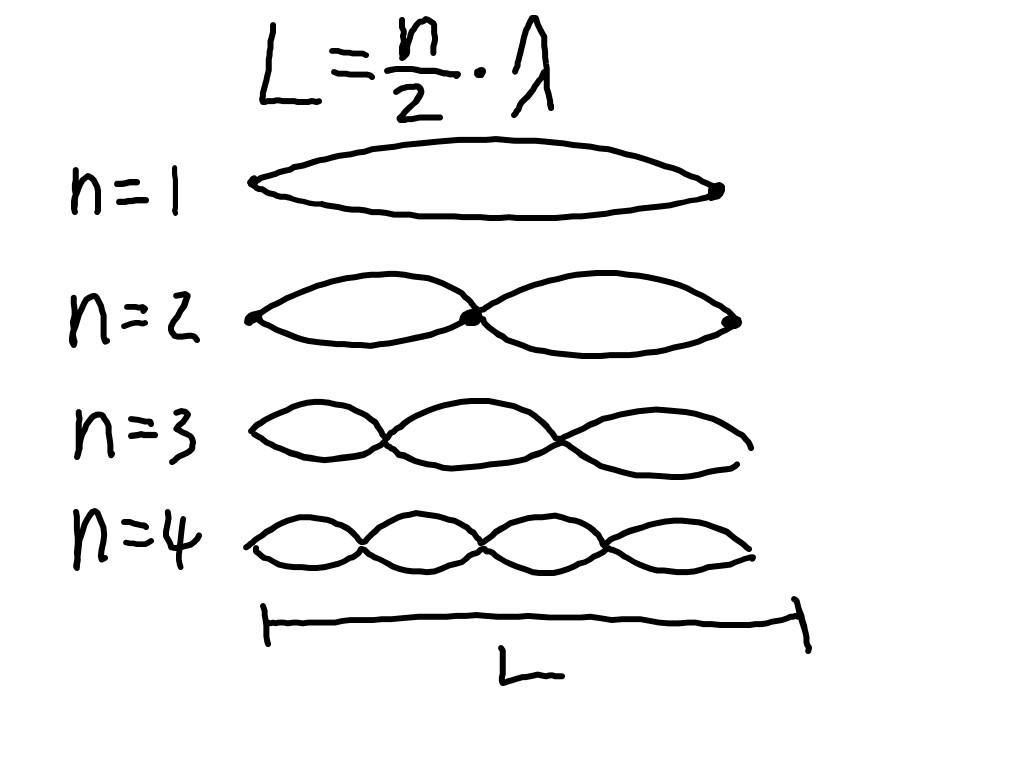
Waves Mind Map
FAQ
6. What is the difference between a node and an antinode?
A node is a point on a standing wave with minimal amplitude (ideally zero displacement), while an antinode is a point with maximum amplitude. Think of a guitar string: the points where the string barely moves are nodes, and the points where it moves the most are antinodes.
7. Can a traveling wave have nodes?
While we don't typically talk about nodes in a traveling wave (since it's constantly moving), we can talk about the distance between points of zero displacement that would be nodes if the wave were stopped. This distance is half the wavelength.
8. Why are nodes important?
Nodes are crucial for understanding and manipulating wave behavior. They play a key role in musical instruments, antenna design, microwave ovens, and many other applications where controlling wave patterns is essential. The specific location of nodes can drastically affect the energy distribution in a system. Without knowledge of them, controlling wave functions wouldn't be nearly as precise, for better or worse.

Standing Wave Nodes And Antinodes