Heartwarming Tips About How To Tell If Two Vectors Are Parallel, Orthogonal, Or Neither
Unraveling Vector Relationships
1. Understanding Vector Orientations
Vectors, those mathematical arrows with direction and magnitude, aren't just floating around aimlessly. They have relationships! Sometimes they're in perfect alignment, sometimes they're at right angles, and sometimes they're, well, just doing their own thing. Figuring out those relationships — whether two vectors are parallel, orthogonal (perpendicular), or neither — is a fundamental skill in various fields, from physics to computer graphics. So, let's dive into how you can decode their orientations.
The key thing to remember is that the relationship between two vectors is defined by their direction. Magnitude (length) doesn't matter when determining parallelism or orthogonality. Think of it like two people walking: whether they are taking baby steps or running a marathon, if they're heading in the same direction, they're still going parallel!
We'll explore the mathematical tools you need: dot products and scalar multiples. Don't worry, it's not as scary as it sounds. We'll break it down with clear explanations and examples. Prepare to become a vector relationship whisperer!
This isn't just abstract math; it has real-world applications. Imagine you're programming a game, and you need to make sure a missile follows a specific trajectory. Understanding vector relationships helps you calculate the missile's direction and speed accurately. Or, picture designing a bridge where you need to ensure the support beams are perfectly perpendicular to the road surface for maximum stability. Vectors are everywhere!

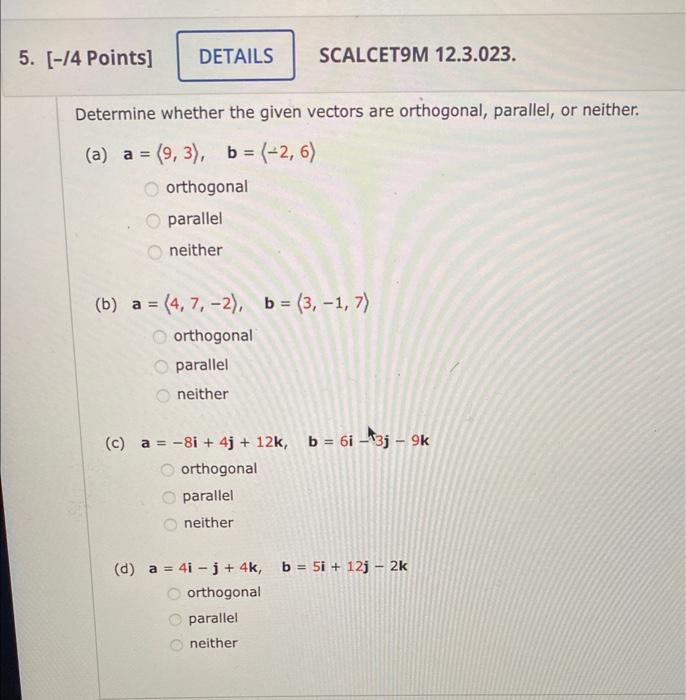
How To Find The Angle Between Two Vectors And Classify As Parallel
Parallel Vectors
2. Identifying Parallelism Through Scalar Multiples
Parallel vectors are like two trains traveling on tracks that run alongside each other: they might be going at different speeds, but they're heading in the same direction (or opposite directions). Mathematically, this means one vector is a scalar multiple of the other. In plain English, you can get one vector by multiplying the other by a number (a scalar).
Let's say we have vector a = (2, 4) and vector b = (4, 8). Notice anything? If you multiply vector a by 2, you get vector b. Therefore, b = 2 a. This means a and b are parallel. Its just that vector b is twice as long as vector a, but pointing in the same direction.
However, here's a sneaky twist: If the scalar is negative , the vectors are still parallel, but they point in opposite directions. These are called anti-parallel vectors. For example, if c = (-2, -4), then c = -1 a. Vector c is parallel to a, but it's going the other way.
So, to determine if two vectors are parallel, try to find a scalar that relates them. If you can find a scalar (positive or negative) that turns one vector into the other, congratulations! You've got yourself some parallel vectors. If you cannot find such scalar, the vectors are not parallel to each other.
Orthogonal Vectors
3. Spotting Orthogonality with the Dot Product
Orthogonal vectors, also known as perpendicular vectors, are vectors that meet at a right angle (90 degrees). These are crucial in geometry and physics. The most reliable way to check for orthogonality is by using the dot product.
The dot product of two vectors, let's say u = (u1, u2) and v = (v1, v2), is calculated as: u v = (u1 v1) + (u2 v2). The magic happens when the dot product equals zero. If u v = 0, then u and v are orthogonal!
Let's illustrate this. Consider vector u = (3, 2) and vector v = (-2, 3). Their dot product is (3 -2) + (2 3) = -6 + 6 = 0. Boom! These vectors are orthogonal.
Think of it like this: orthogonal vectors are completely independent of each other in terms of direction. One vector's direction has no component in the direction of the other. This independence is what makes the dot product zero. If the dot product is anything other than zero, the vectors aren't perfectly perpendicular.

Neither Parallel Nor Orthogonal
4. When Vectors March to Their Own Beat
Now, what happens when two vectors aren't parallel and aren't orthogonal? Well, they're just...neither! They're simply pointing in different directions with no special relationship between them. Most pairs of randomly chosen vectors will fall into this category.
To identify this, first, try to see if one vector is a scalar multiple of the other. If you cant find a scalar that makes them equal (or negative of each other), they are not parallel. Next, calculate the dot product. If the dot product is not equal to zero, they are not orthogonal. Thus, if both tests fail, you're dealing with vectors that are neither parallel nor orthogonal.
Imagine two people walking in a park; one is heading towards the pond at a 45-degree angle, and the other is going to the playground at a 70-degree angle. They aren't aligned, and they aren't at a perfect right angle. They're just going their separate ways.
In practical terms, these "neither" vectors might still have some relationship, just not a mathematically "special" one. You can still calculate the angle between them (using some trigonometry, which is a topic for another day!). But for the purposes of this article, they're simply categorized as neither parallel nor orthogonal.
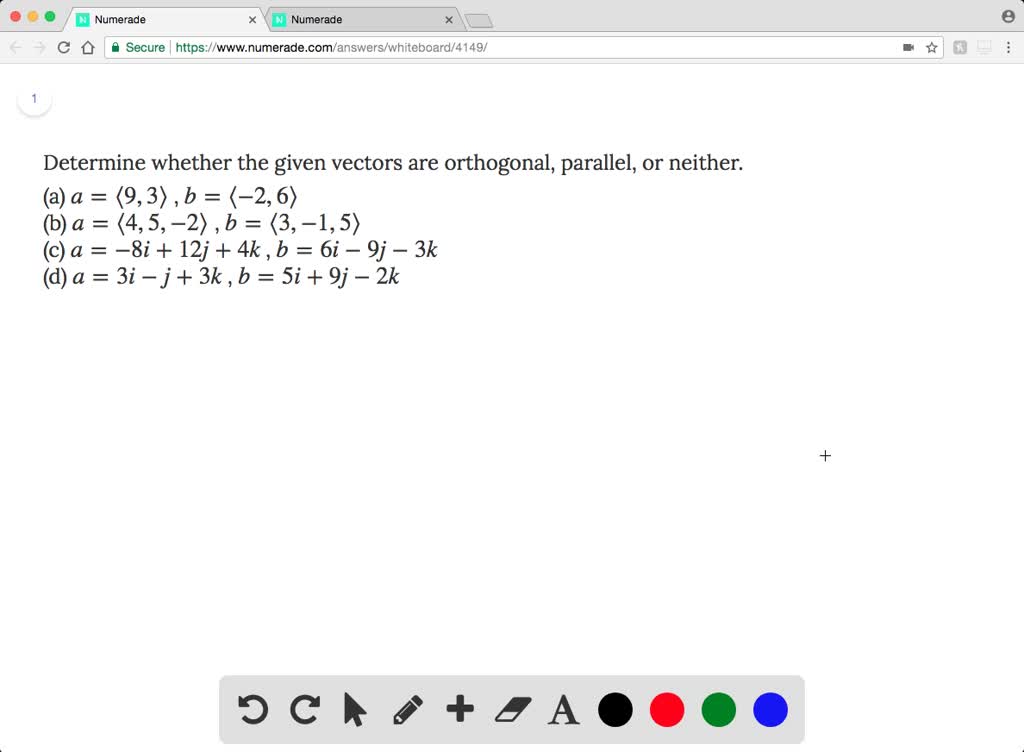
Putting it All Together
5. A Summary of Vector Relationships and Their Determinations
Okay, so how do we quickly determine the relationship between two vectors? Let's recap the steps:
- Check for Parallelism: Can you multiply one vector by a scalar to get the other? If yes, they're parallel (or anti-parallel if the scalar is negative).
- Check for Orthogonality: Calculate the dot product of the two vectors. If it equals zero, they're orthogonal.
- If both checks fail: The vectors are neither parallel nor orthogonal.
With practice, you'll be able to eyeball vectors and quickly make an educated guess about their relationship. But always remember to double-check with the math to be sure. A little calculation can prevent a lot of errors!
Knowing how to identify vector relationships opens up a new world of possibilities in various fields, like physics simulations, computer graphics, and even data analysis. Vectors are a fundamental tool for representing direction and magnitude, and understanding their relationships is key to solving many real-world problems.
So, next time you see a couple of vectors hanging out, you'll know exactly how to determine if they are best friends, bitter enemies, or just acquaintances passing by in the mathematical world.

Linear Algebra Orthogonality Of Zero Vector Relative To Nonzero
Frequently Asked Questions About Vector Relationships
6. Addressing Common Queries About Vector Orientations
Here are some frequently asked questions to solidify your understanding of vector relationships:
Q: Can a zero vector be parallel or orthogonal to another vector?A: A zero vector (a vector with all components equal to zero) is considered parallel to any vector because you can multiply any vector by zero to get the zero vector. The zero vector is also considered orthogonal to every vector because the dot product of the zero vector with any vector is always zero.
Q: What if I have vectors in 3D space (or higher dimensions)? Does the same logic apply?A: Absolutely! The fundamental principles remain the same regardless of the number of dimensions. For parallelism, you still look for scalar multiples. For orthogonality, you calculate the dot product, extending the formula to include all components. For example, in 3D space, if u = (u1, u2, u3) and v = (v1, v2, v3), then u v = (u1 v1) + (u2 v2) + (u3 * v3). If this sum is zero, the vectors are orthogonal.
Q: Why is the dot product zero for orthogonal vectors?A: The dot product can also be expressed as |u| |v| cos(), where |u| and |v| are the magnitudes of the vectors, and is the angle between them. When the vectors are orthogonal, the angle is 90 degrees (or /2 radians), and cos(90) = 0. Therefore, the dot product becomes zero, regardless of the magnitudes of the vectors.